Cosmology View

My views on Cosmology and Physics

site navigation menu
 

Book by David Michalets

Review of Einstein's 1920 Book on Relativity  (from Translation)

An (original) line precedes original content from the source.

A (remark) line precedes my remark from my review of the preceding original content.

My remark applies to only this section of the original.

Section XXV of 35
 

XXV. GAUSSIAN CO–ORDINATES

(original)

ACCORDING to Gauss, this combined analytical and geometrical mode of handling  the problem can be arrived at in the
following way. We imagine a system of arbitrary curves (see Fig. 4) drawn on the surface of the table. These we designate as u-curves, and we indicate each of them by means of a number.
The curves u = 1, u = 2 and u = 3 are drawn in the diagram. Between the curves u = 1 and u = 2 we must imagine an infinitely large number to be drawn, all of which correspond to real numbers lying between 1 and 2. We have then a system of u-curves, and this "infinitely dense" system covers the whole surface of the table. These u-curves must not intersect each other, and through each point of the surface one and only one curve must pass. Thus a perfectly definite value of u belongs to every point on the surface of the marble slab. In like manner we magine a system of v-curves drawn on the surface. These satisfy the same conditions as the u-curves, they are provided with numbers in a corresponding manner, and they may likewise be of arbitrary shape. It follows that a value of u and a value of v belong to every point on the surface of the table. We call these two numbers the co-ordinates of the surface of the table (Gaussian co-ordinates). For example, the point P in the diagram has the Gaussian co-rdinates u = 3,v = 1. Two neighbouring points P and P' on the surface then correspond to the co-ordinates P: P': u, v
u + du, v + dv,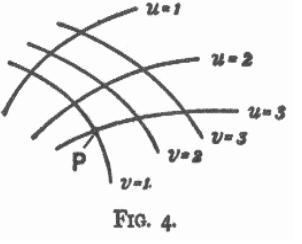

awhere du and dv signify very small numbers. In a similar manner we may indicate the distance (line-interval) between P  nd P', as measured with a little rod, by means of the very small number ds. Then according to Gauss we have ,
ds^2 = 2g12 du + 2g du dv + g22 dv^2
where g11, g12, g22, are magnitudes which depend in a perfectly definite way on u and v. The magnitudes g11, g12 and  22 determine the behaviour of the rods relative to the u-curves and v-curves, and thus also relative to the surface of the table. For the case in which the points of the surface considered form a Euclidean continuum with reference to the measuring-rods, but only in this case, it is possible to draw the u-curves and v-curves and to attach numbers to them, in such a manner, that we simply have:
.
2 2 2 ds^2 = du^2 + dv^2
Under these conditions, the u-curves and v-curves are straight lines in the sense of Euclidean geometry, and they are perpendicular to each other.
Here the Gaussian co-ordinates are simply Cartesian ones. It is clear that Gauss co-ordinates are nothing more than an association of two sets of numbers with the points of the surface considered, of such a nature that numerical values differing very slightly from each other are associated with neighbouring points "in space."
So far, these considerations hold for a continuum of two dimensions. But the Gaussian method can be applied also to a continuum of three, four or more dimensions. If, for instance,
a continuum of four dimensions be supposed available, we may represent it in the following way. With every point of the continuum we associate arbitrarily four numbers, x1, x2, x3, x4,which are known as "co-ordinates." Adjacent points correspond to adjacent values of the coordinates. If a distance ds is associated with the adjacent points P and P', this distance being measurable and well-defined from a physical point of view, then the following formula holds:
ds^2 = g11 dx^2 + 2g12 dx1 dx2 . . . . + g44 dx4^2 ,
where the magnitudes g11, etc., have values which vary with the position in the continuum. Only when the continuum is a Euclidean one is it possible to associate the co-ordinates x1 . . x4 with the points of the continuum so that we have simply
ds^2 = dx1^2 + dx2^2 + dx3^2 + dx4^2 .
In this case relations hold in the four-dimensional continuum which are analogous to those holding in our three-dimensional measurements. However, the Gauss treatment for 2 ds which we have given above is not always possible. It is only possible when sufficiently small regions of the continuum under consideration may be regarded as Euclidean continua. For example, this obviously holds in the case of the marble slab of the table and local variation of temperature.
The temperature is practically constant for a small part of the slab, and thus the geometrical behaviour of the rods is almost as it ought to be according to the rules of Euclidean geometry.
Hence the imperfections of the construction of squares in the previous section do not show themselves clearly until this construction is extended over a considerable portion of the surface of the table.
We can sum this up as follows: Gauss invented a method for the mathematical treatment of continua in general, in which "size-relations"
("distances" between neighbouring points) are defined. To every point of a continuum are assigned as many numbers (Gaussian co-ordinates) as the continuum has dimensions. This is done in such a way, that only one meaning can be attached to the assignment, and that numbers (Gaussian co-ordinates) which differ by an indefinitely small amount are assigned to adjacent points. The Gaussian co-ordinate system is a logical generalisation of the Cartesian co-ordinate system. It is also applicable to non-Euclidean continua, but only when, with respect to the defined "size" or "distance," small parts of the continuum under consideration behave more nearly like a Euclidean system, the smaller the part of the continuum  under our notice.


(remark)

When starting with a geometry, like gaussian coordinates,  this section is about only an observer. Only an observer uses a geometry and coordinate system, to make measurements.

Everything else in the universe is an object subject to the external fundamental forces.

For celestial measurements, an observer would probably begin with the celestial coordinate system. The Gaussian system is used by few, and well understood by fewer.


Go to Table of Contents, to read a specific section.

last change 05/07/2022